
Light-emitting diodes, or LEDs, are at the forefront of modern illumination for every purpose imaginable, because of their high efficiency, long life, fast switching capabilities, and vibrant color spectrum possibilities. Every year, smaller and smaller LEDs are developed that produce more and more light, as a function of the power consumed. The high brightness potential is one of the main reasons many auto manufacturers are replacing incandescent lighting fixtures with LED versions, whether it is the 3rd brake light, tail lights, interior lighting, or even the headlights.
In this page, we will be primarily discussing LEDs, meaning the individual LEDs themselves, which are sometimes referred to as "chips." When reading, keep in mind that an "LED bulb" is a full electrical circuit, including multiple LEDs and other components, which is then fitted to a base. Please see the LED Design page for more information on how LED chips are designed into LED bulbs.
Jump to a Section
Measuring Brightness
Lumens

The brightness of a light is usually measured in lumens, or the total amount of light generated. Lumens are derived from luminous flux, which is the total power of light, which is why high-power bulbs are sometimes called "high-flux," To measure lumens, an LED is placed inside a sealed reflective sphere, known as an integrating sphere, and its light is bounced around in all directions in the sphere (integrated) so its flux can be measured at one point, and calculated into lumens based on the size of the sphere. LEDs vary widely in their brightness potential, and can be "dimmed" by running at a lower current.
Note: the reason some commercial LED bulbs cannot be dimmed is because of the power controller in the bulb, not the LEDs themselves. All LEDs can be dimmed with the right power supply.
Candelas
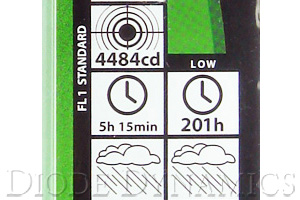
You may see some LED lights measured in mcd, or millicandelas. The candela is a measurement of the total light generated and focused in one particular direction. This is why you might see a flashlight rated in candelas rather than lumens- it is more useful to know how much light is focused with the flashlight, not the total light, which includes some light dispersed in all directions.
Lux
Another measurement of light is lux, or the light measured in 1 square meter of output area. For example, if you mark off one square meter on your garage, and measure all the light that goes into that area when your car is exactly 10 feet away from it, you would have the lux measurement at 10 feet, straight-on, of your headlights. As you can see though, it's somewhat difficult to measure lux along a particular output, and you must factor in how far away the source of light is. Lux ratings are useful for light housing manufacturers, as they want the highest lux available straight-on to light the road ahead, but they also want some lux measurement downwards directly on the road.
Lumens vs. Lux: It's All About the Housing
Just because a bulb has a higher lumen output, doesn't mean it will "appear" brighter when you look directly at it. Looking directly at the source of light will tell you the lux, or amount of light that specifically reaches your eye. Some LED bulbs are designed with projectors to focus the light in one direction, and that will make them very bright in one direction, or a high lux, but from another angle, the brightness will decrease sharply.

Lux is not a good measurement for automotive use, because automotive housings are designed for use with incandescent bulbs, which evenly distribute light in all directions. Your different housings are designed for different purposes- for example, a headlight will collect and focus the light forwards, and a sidemarker will collect and disperse the light to as much area as possible. Because the housing can modify the light path of the bulb, the same bulb can look completely different in two different housings.
Most older LEDs have high lux in one direction, as the light is focused, but they don't "fill up" the housing. I'm sure we've all seen poorly-designed LED bulbs on the road, where you can see high lux, but low total lumens. Remember, just because a bulb "looks bright" does not mean it will perform better.
Sometimes high lux is good: you might see us refer to an LED bulb with an integrated focusing lens as "high-lux," which might be great for backup light applications, where you just want light directed behind your vehicle. However, for most replacement lights, they should evenly distribute the light, just like the factory incandescent. That way, the light housing can do its job and distribute the total light in the way it is designed. High lux is not always beneficial, but it's always best to have as many lumens as possible!
Since Diode Dynamics products are designed to replace bulbs in a variety of manufacturer housings, we only provide lumen measurements for our products, to give our customers the best idea of the total light output. We have a scientific integrating sphere to provide accurate measurements to our customers.
Generating Light
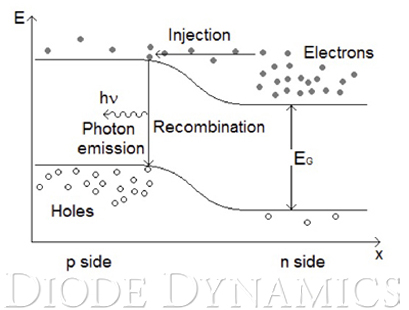
LEDs are a type of semiconductor diode. (Now you know the secret of where our name comes from!) This means they use semiconductor materials to allow electrons to pass through a p-n junction. When electrons of the n-type semiconductor fill the holes of the p-type semiconductor, energy is released as photons, or light.
There must be a higher voltage potential on the p-side of the LED than the n-side for this atomic interaction to work, which is why all LEDs are polar, meaning they have specific polarity. If you see a "non-polarity LED bulb," the power controller that is built into the bulb is non-polarity, not the individual LED chips themselves.
Once the power is in the correct direction to flow through the LED, the brightness is determined by the current, or the speed of the flow of power. The more electrons filling holes, the more photons released, and the higher the brightness output. Of course, LEDs can only withstand a maximum current and voltage before they "blow," so it is important to carefully control this through the correct supply of power.
Supplying Power
Since automotive power is 12V, and LEDs generally run best on 2-4V, depending on color, you must use resistors or other components to drop the voltage to a level the LED can work with. This is why you cannot simply plug a basic LED directly into your socket, or connect it to a 9V battery. The manufacturer will determine what the nominal (normal) voltage is to run a specific LED, known as the "forward voltage." For example, a blue LED might be rated as 3.0-3.2V. Adjusting the voltage lower or higher will change the brightness, but only because it also changes the current- higher voltage means the current will increase in an LED.
After ensuring that you have the correct voltage available to the LED, the next step is determining current. This is measured in amperes, or amps, but since it's such a small amount of current, LEDs will be rated in milliamps (mA). There are 1000 milliamps in an amp. The more current, the brighter the LED, but there is always a maximum "running" or "constant" current, which is the max you should run the LED at, and usually there is a max "peak" current, which is the highest current the LED can withstand before completely failing.
As LEDs have evolved, they have generally required higher tolerances in terms how much current they require and can handle. The oldest LEDs had a large range of current where they would light up, and could withstand swings in current without too much of a detrimental effect. The newest LEDs can run on much higher current, to generate a much greater amount of light, but cannot handle such drastic swings while they are running, and will fail if they are put under too much stress. For this reason, it is critical to provide the correct current and voltage to LEDs, especially the newest, high-power ones.
LED Efficiency
The voltages and currents of different LEDs will vary, so to directly compare LEDs, the measure of total power consumed is also provided by the manufacturer. Power is calculated as (Voltage x Current), so an LED that is running on 20mA (.02A) and 3V would be consuming 0.06W of power.

To compare this to an incandescent bulb, though, we need to look at the total power consumed by a full LED bulb. Like we mentioned, the whole LED bulb includes other components to regulate the voltage to the LEDs, and might have more than one LED. If you have three LEDs running on 20mA each, you would need to supply 60mA total, and drop the voltage from 12V, so the whole bulb would consume power of (12V x 60mA) = .72W. As you can see, a lot of power is consumed in dropping the voltage down, and we need more power to run more LEDs. Still, this example of a 60mA bulb is actually realistic for a standard 194-bulb replacement. The incandescent 194 bulb consumes 5W of power!

When we talk about efficiency, we refer to the amount of light generated for each watt of power consumed. The device will convert the power to heat and light. In the above example, if the total output of the LED and incandescent bulb is 50 lumens, we could say that the LED has an efficiency of 50/.72, or about 70 lumens per watt. The incandescent bulb, on the other hand, will have an efficiency of 50/5 = only 10 lumens/watt! The LED is much more efficient at converting power to light.

LEDs also "run cooler" because they are more efficient —they don't convert as much of the power to heat as incandescent bulbs do. LEDs still convert power to heat, though- and some LEDs will get very hot! Specifically, in high-power LEDs, heat becomes a big problem. You must keep the LED cool enough to keep everything running properly, and this is one of the primary reasons poorly-designed LED bulbs can fail.

Rating and Describing LEDs
As we discussed, LEDs are designed to run at a nominal (normal) voltage and current for optimal operation. Manufacturers generally state the "nominal" numbers as a perfect scenario, where you can get rid of all excess heat and there won't be any changes in power, or "spikes" that the LED has to deal with.

In automotive applications, however, LEDs have to deal with large voltage swings as the alternator keeps re-charging the battery (only 1V change is considered a huge spike for an LED) and the small size of automotive bulbs means that LEDs have to be packed into a small space, which means they are not going to be able to cool themselves very well- nothing like the scenario in which the manufacturer "rated" the LEDs.
Therefore, when designing bulbs for automotive use, designers configure LED bulbs so that each LED on the bulb will run at a specifically-calculated voltage and current. By lowering the power supplied to an LED, you can get longer life out of an LED, and it will not get as hot, but it won't be quite as bright. You can also ensure the LED won't go out if the voltage suddenly rises to 14V for a few seconds, for example.

Most designers still use the nominal ratings of each individual LED chip to describe the whole bulb, especially in high-power bulbs. For example, an 80W bulb might use 16 individual 5W-rated LEDs, so the designer will call it an "80W bulb." However, the LEDs are not going to actually consume 80W of power. Instead, the LEDs are running at a much lower actual power, in order to manage the heat and prevent them from failing prematurely. This might be called "Actual Power Consumption" or "Real Power." The Real Power consumed by the whole bulb may only be about .5 amps. Automotive LEDs are designed to run at much lower than their "full potential," in order to improve reliability.

When purchasing LED bulbs, the "80W" should only be considered the name of the bulb, not a description of its electrical properties, or even how bright it is! Yes, an "80W" bulb is probably going to be brighter than a "10W" bulb, but the total brightness all depends on how the bulb is designed. How much power is actually being used by the LEDs on that bulb? An "80W" bulb from one supplier may be half the brightness as an "80W" bulb from another supplier. Make sure you compare the Real Power, or better yet, just find an actual lumen measurement to determine total brightness.
Lumen Lies
Watch out! Many suppliers will take the inaccurate "80W" power rating, described in the previous section, and will just assume an efficiency for that bulb depending on the type of LED. For example, they might say, "high-power LED bulbs usually emit about 10 lumens per watt, so this bulb will be about 800 lumens!" This is a complete guess, and is likely completely inaccurate.
Why do they do this? It is quite expensive to test actual lumen outputs — integrating spheres can cost up to $100,000 — but suppliers know it is a great way to compare bulbs, so they will "calculate" or "approximate" the lumen output for you. Sneaky, huh? If you see what seems like a completely arbitrary lumen rating, such as "1200 lumens," it probably is just that- a completely inaccurate guess.
Make sure your supplier provides "Measured Lumens," not "Calculated," "Estimated," or "Approximate." If it doesn't say "measured," it's probably not accurate! Stay away from any dishonest companies that offer "calculated lumens" at all costs!














